نصيحة 1: كيفية تحديد نوع المثلث
نصيحة 1: كيفية تحديد نوع المثلث
المثلث هو أبسط المضلعات. وهو يتألف من ثلاث نقاط الكذب في طائرة واحدة، ولكن ليس خط مستقيم واحد، زوجي متصلة من قبل قطاعات. ومع ذلك، يمكن أن تكون المثلثات مختلفة تماما، ونتيجة لذلك، لها خصائص مختلفة.
تعليمات
1
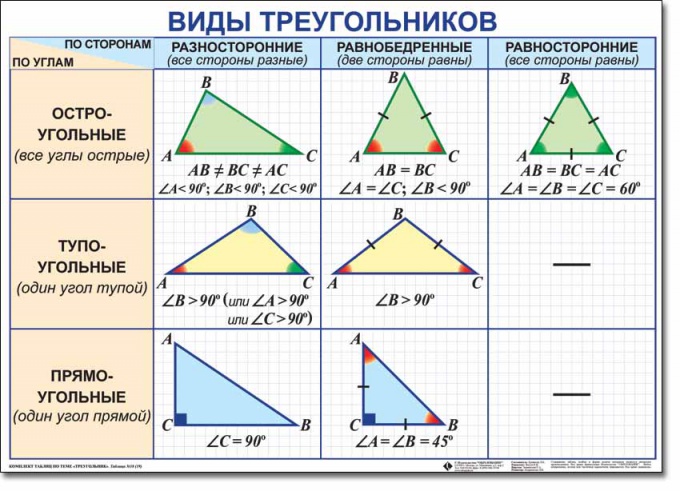
ومن المعتاد أن واحد من ستة نوع مثلثات. في قلب هذا التقسيم تصنيفين: في الزوايا وعلى الجانبين. التصنيف حسب أنواع الزوايا يفترض تقسيم المثلثات إلى حادة، مستطيلة و منفرجة. التصنيف حسب نسبة الجانبين يقسم المثلثات إلى تنوعا، متساوية الأضلاع و إسوسليز. و كل مثلث ينتمي في وقت واحد إلى نوعين. على سبيل المثال، يمكن أن تكون مستطيلة وتنوعا في نفس الوقت.
2
تعريف النموذج مثلث حسب نوع الزوايا، كن حذرا جدا. سيتم استدعاء مثلث منفرجة، التي واحدة من زوايا حادة، وهذا هو، أكثر من 90 درجة. ويمكن حساب مثلث مستطيل بحضور زاوية واحدة مباشرة (تساوي 90 درجة). ومع ذلك، من أجل تصنيف المثلث كما الحادة، وسوف تحتاج للتأكد من أن كل من زواياها ثلاثة حادة.
3
تعريف النموذج مثلث من خلال نسبة من الجانبين، أولا سيكون لديك لتعلم أطوال جميع الأطراف الثلاثة. ومع ذلك، إذا كان شرط من طول الجانبين لا تعطى، يمكن للزوايا مساعدتك. سوف تنوعا يكون مثلث، جميع الجوانب الثلاثة التي لها أطوال مختلفة. إذا كانت أطوال الجانبين غير معروفة، ثم يمكن تصنيف المثلث كما تنوعا إذا كانت كل من زواياها مختلفة. المثلث تنوعا يمكن أن يكون منفتح، مستطيلة وحادة.
4
مثلث إيزوسليس، اثنان منهمثلاثة جوانب منها تساوي بعضها البعض. إذا لم يتم إعطاء أطوال الجانبين لك، تسترشد اثنين من زوايا متساوية. المثلث إيزوسليز، مثل واحد تنوعا، يمكن أن تكون منفرجة، ومستطيلة وحادة الزاوية.
5
يمكن تسمية ما يعادل فقطمثلث، جميع الجوانب الثلاثة التي لها نفس الطول. جميع زواياها هي أيضا مساوية لبعضها البعض، وكل واحد منهم يساوي 60 درجة. ومن ثم فمن الواضح أن مثلثات متساوية الأضلاع هي دائما زوايا حادة.
النصيحة 2: كيفية تحديد المثلث المثلث والزاوية الحادة
أبسط المضلعات هو مثلث. يتم تشكيله مع مساعدة من ثلاث نقاط الكذب في طائرة واحدة، ولكن لا الكذب على خط مستقيم واحد، زوجي متصلة من قبل قطاعات. ومع ذلك، فإن المثلثات من أنواع مختلفة، وبالتالي لها خصائص مختلفة.

تعليمات
1
ومن المعتاد التمييز بين ثلاثة أنواع من المثلثات: منفرجة، حادة ومستطيلة. هذا تصنيف حسب نوع الزوايا. المثلث المثلث هو واحد في واحدة من الزوايا هو حادة. بلونت هي الزاوية، التي هي أكبر من تسعين درجة، ولكن أقل من مائة وثمانين. على سبيل المثال، في أبك المثلث، زاوية أبك هي 65 درجة، زاوية بكا هي 95 درجة، زاوية كاب هو 20 درجة. الزوايا أبك و كاب هي أقل من 90 درجة، ولكن زاوية بكا أكبر، وبالتالي فإن المثلث هو منفتح.
2
المثلث الحاد هو المثلث الذيجميع الزوايا حادة. زاوية حادة هي زاوية أقل من تسعين وأكبر من الصفر درجة. على سبيل المثال، في المثلث أبك، زاوية أبك هي 60 درجة، زاوية بكا هو 70 درجة، زاوية كاب هو 50 درجة. جميع الزوايا الثلاثة أقل من 90 درجة، وبالتالي فإن المثلث هو الزاوية الحادة. إذا كنت تعرف أن جميع جوانب المثلث متساوية، وهذا يعني أن جميع زوايا منه هي أيضا مساوية لبعضها البعض، في حين أنها تساوي ستين درجة. وفقا لذلك، جميع الزوايا في مثلث مثل أقل من تسعين درجة، وبالتالي مثل هذا المثلث هو الزاوية الحادة.
3
إذا كان في المثلث واحدة من الزوايا تساوي تسعين درجة، وهذا يعني أنه لا ينطبق على نوع زاوية واسعة أو إلى نوع الزاوية الحادة. هذا هو المثلث الزاوية اليمنى.
4
إذا تم تحديد شكل المثلث حسب العلاقةالأطراف، وسوف تكون متساوية الأضلاع، تنوعا و إيزوسليس. في مثلث متساوي الأضلاع، جميع الأطراف متساوية، وهذا، كما اكتشفت، يشير إلى أن المثلث هو الزاوية الحادة. إذا كان المثلث له سوى جانبين أو الجانبين ليست متساوية مع بعضها البعض، يمكن أن يكون منفتح، ومستطيلة، وحادة. وبالتالي، في هذه الحالات من الضروري حساب أو قياس الزوايا واستخلاص الاستنتاجات، وفقا للنقاط 1 أو 2 أو 3.
نصيحة 3: أي المثلثات تسمى متساوية
والمساواة بين اثنين أو أكثر من المثلثات تتوافق مع الحالة عندما تكون جميع الأطراف وزوايا هذه المثلثات متساوية. ومع ذلك، هناك عدد من المعايير الأكثر بساطة لإثبات هذه المساواة.

سوف تحتاج
- كتاب على الهندسة، ورقة من الورق، قلم رصاص بسيط، منقلة، حاكم.
تعليمات
1
افتح الكتاب الهندسي للصف السابععلى علامات المساواة بين المثلثات. سترى أن هناك عددا من السمات الأساسية التي تثبت المساواة بين المثلثات اثنين. وإذا كان هناك مثلثان يتم التحقق من مساواتهما تعسفيا، فهناك ثلاثة علامات أساسية للمساواة. وإذا كانت بعض المعلومات الإضافية عن المثلثات معروفة، فإن الميزات الثلاث الرئيسية تستكمل بعدة أشياء أخرى. وينطبق ذلك، على سبيل المثال، على حالة المساواة بين المثلثات القائمة على الزاوية اليمنى.
2
قراءة القاعدة الأولى حول المساواةمثلثات. كما تعلمون، فإنه يسمح لك للنظر المثلثات متساوية إذا كنت تستطيع أن تثبت أن أي زاوية واحدة واثنين من الجانبين المتاخمة لمثلثين متساويين. من أجل فهم كيفية عمل هذا القانون، واستنادا إلى ورقة من الورق مع منقلة اثنين من زوايا محددة متطابقة شكلت من قبل اثنين من الأشعة المنبعثة من نقطة واحدة. قياس حاكم مع نفس الجانبين من أعلى الزاوية المرسومة في كلتا الحالتين. باستخدام المنقلة، وقياس زوايا المثلثات شكلت اثنين، تأكد من أنها متساوية.
3
من أجل عدم اللجوء إلى هذه العمليةتدابير لفهم المساواة المثلث، قراءة دليل على أول علامة على المساواة. والحقيقة هي أن كل قاعدة على المساواة بين المثلثات لديها دليل نظري صارم، هو ببساطة ليست مريحة لاستخدامها من أجل حفظ القواعد.
4
قراءة علامة الثانية من المساواة بين المثلثات. وينص على أن مثلثين متساويان إذا كان أي جانب واحد وزاويتين متجاورتين لمثلثين متساويين. من أجل تذكر هذه القاعدة، تخيل الجانب المرسوم من المثلث واثنين من الزوايا المجاورة. تخيل أن أطوال جانبي الزوايا تزداد تدريجيا. في النهاية، فإنها تتقاطع، وتشكيل زاوية ثالثة. في هذه المهمة العقلية، من المهم أن نقطة تقاطع الجانبين التي تتزايد عقليا، فضلا عن زاوية الناتجة، يتم تحديد فريد من قبل الطرف الثالث وزوايا المتاخمة اثنين.
5
إذا لم تعط أي معلومات حول الزواياثم استخدم العلامة الثالثة من المساواة بين المثلثات. ووفقا لهذه القاعدة، يعتبر المثلثان متساويين إذا كانت جميع الجوانب الثلاثة لأحدهما تساوي الجوانب الثلاثة المقابلة للطرف الآخر. وهكذا، تقول هذه القاعدة أن أطوال جانبي المثلث تحدد بشكل فريد جميع زوايا المثلث، وبالتالي فهي تحدد بشكل فريد المثلث نفسه.







